Significance
The advent of finite element methods, powered with modern computing power, has ultimately provided tools applicable in both modern mathematics and physics. Among other uses, finite element methods are presently the preferred tool for solving 3D elasticity problems in solids. For such purposes, an 8-node hexahedral element is widely used for modeling and analysis. However, the standard 8-node displacement-based element suffers from severe loss of accuracy caused by locking. Ideally, such finite element based solutions should be stable but the aforementioned situation has proven otherwise.
Previous studies have highlighted that the stability and accuracy of finite element solutions can be assessed by investigating whether the ellipticity, continuity and relevant inf-sup conditions are satisfied. However, proving analytically that the conditions are satisfied for an element used in the analysis of incompressible media and plate and shell structures can be extremely difficult. Consequently, a numerical inf-sup test becomes necessary in order to obtain insight regarding the element’s formulation.
Recently, Professor Klaus-Jürgen Bathe at Massachusetts Institute of Technology in collaboration with Dr. Yeongbin Ko, a research engineer at ADINA R & D Inc (specializes in computational mechanics) introduced a valuable approach where they used inf-sup tests to obtain more insight regarding the reliability of the recently proposed 8-node hexahedral element: the 3D-MITC8 element. In particular, they focused on assessing 8-node hexahedral 3D solid elements, with much attention on the locking behavior in volumetric, shear, membrane, and pinching actions. Their work is currently published in the research journal, Computers and Structures.
In their study, the authors considered the standard 8-node displacement-based element, the 8-node element with incompatible modes and the recently proposed 3D-MITC8 element. The investigation focused on whether the aforementioned elements lock in the analyses of incompressible media, and in the analyses of plates, and shells, and on whether such locking can be seen using the inf-sup condition on the “complete matrix” described by displacement degrees of freedom only. The authors considered various geometries, boundary conditions, material properties and thicknesses to see the behaviors of the inf-sup values as the meshes were refined.
The two scholars observed that the calculated inf-sup curves corresponded well to the convergence curves obtained for the elements in comparison to results from other convergence studies. Moreover, as anticipated, the researchers recorded that they were able to read from the inf-sup curves that the H8 element was locking, in all cases considered. Furthermore, in the analysis of incompressible media, the H8I9 and 3D-MITC8 elements showed a similar performance, but in the analysis of plates considering shear locking the 3D-MITC8 element performed best.
In summary, the Bathe and Ko study demonstrated a finite element-based numerical procedure excellent in elucidating on the reliability of 8-node hexahedral elements using inf-sup tests. Generally, the researchers were able to show that the 3D-MITC8 element performed better than the incompatible modes element in plate bending problems, and therefore can be used with a small modification in the solution of thick or moderately thick curved shell structures.
In a statement to Advances in Engineering, the authors commented on their study: “In the continuous strive for more effective finite element analyses, notably much faster solutions for the democratization of finite element methods for designers, it is of paramount importance to not by-pass the need for reliable schemes. This study focuses on testing various element formulations for their reliability and shows how other formulations can be tested.”
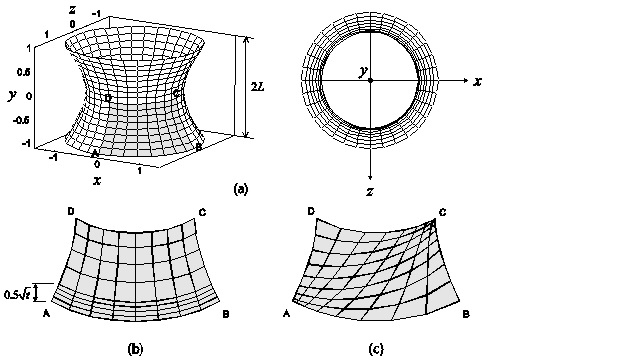
Figure 1 Hyperboloid shell ( L=1.0, t = 1/10, 1/100, 1/1000 or 1/10000, E = 1.0 and v = 0.0 ). (a) Geometry description. (b) Graded regular mesh (8×8 elements). (c) The distorted mesh of Fig. 12(b) (8×8 elements).

Figure 2 Inf-sup convergence curves for the hyperboloid shell using (a) regular and (b) distorted meshes
Reference
Yeongbin Ko, Klaus-Jürgen Bathe. Inf-sup testing of some three-dimensional low-order finite elements for the analysis of solids. Computers and Structures, volume 209 (2018) page 1–13.
Go To Computers and Structures Advances in Engineering Advances in Engineering features breaking research judged by Advances in Engineering advisory team to be of key importance in the Engineering field. Papers are selected from over 10,000 published each week from most peer reviewed journals.
Advances in Engineering Advances in Engineering features breaking research judged by Advances in Engineering advisory team to be of key importance in the Engineering field. Papers are selected from over 10,000 published each week from most peer reviewed journals.



